講義
サイン波(純音)の式
講義の第1の目標は、数学嫌いを含む全員に、サイン波の式を納得してもらう事でした。
y (t ) = A sin( 2πft )
サイン波(すなわち純音)の理解は、音の科学で必須の第一歩です。英語で最初にABCを覚えるのと同じレベルの重要さです。
サイン波の振動を耳で聞いた音が純音 (pure tone)です。純音は、すべての音の基本です。
サイン関数は、単位円で考えるとわかりやすいです。
◯ 単位円の点がぐるぐる回るとき、そのy座標を追ったのがサイン関数
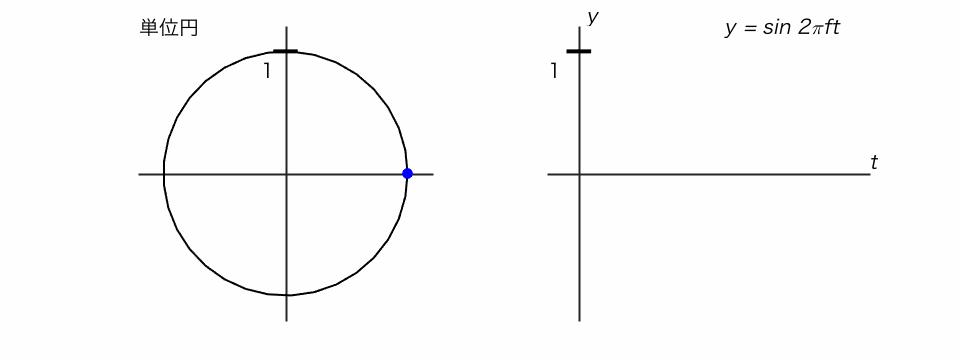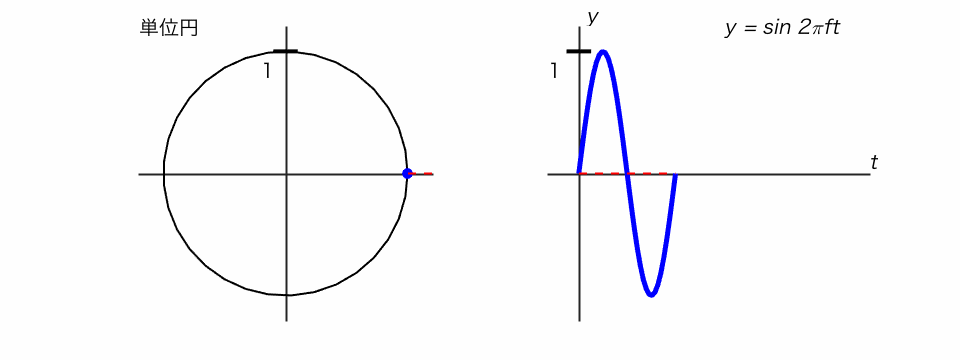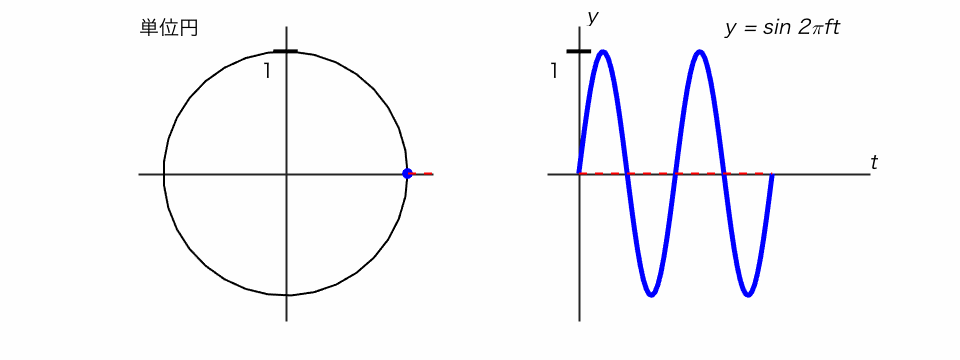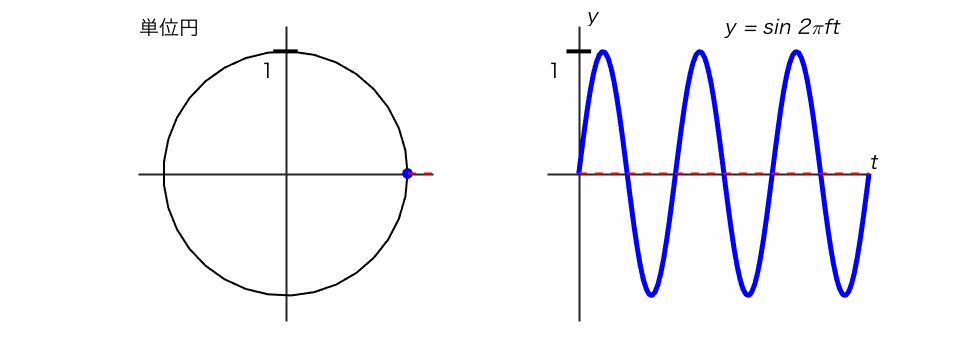
音の三要素を数式で表す
講義の第2の目標は、音の3要素(大きさ、高さ、音色)を数式で表すことでした。大きさと高さは、サイン波の振幅(A)と周波数(f)にそれぞれ対応しています。音色は、サイン波の足し合わせ(複合音)で考えます。
◯ 振動の周波数 f が高い(回転が速い)と、高い音になります。
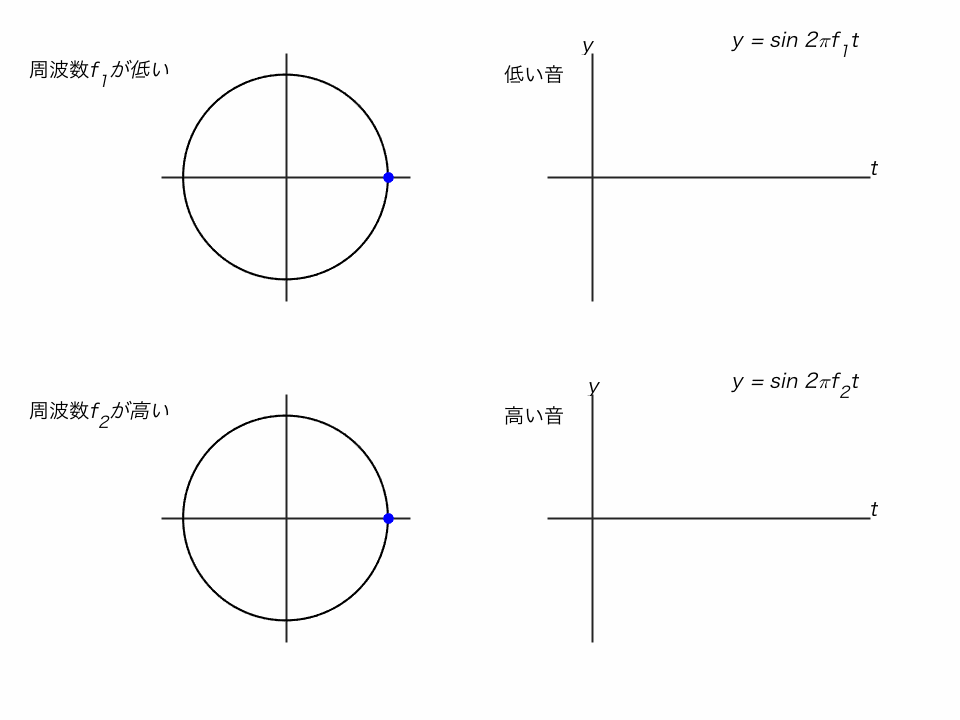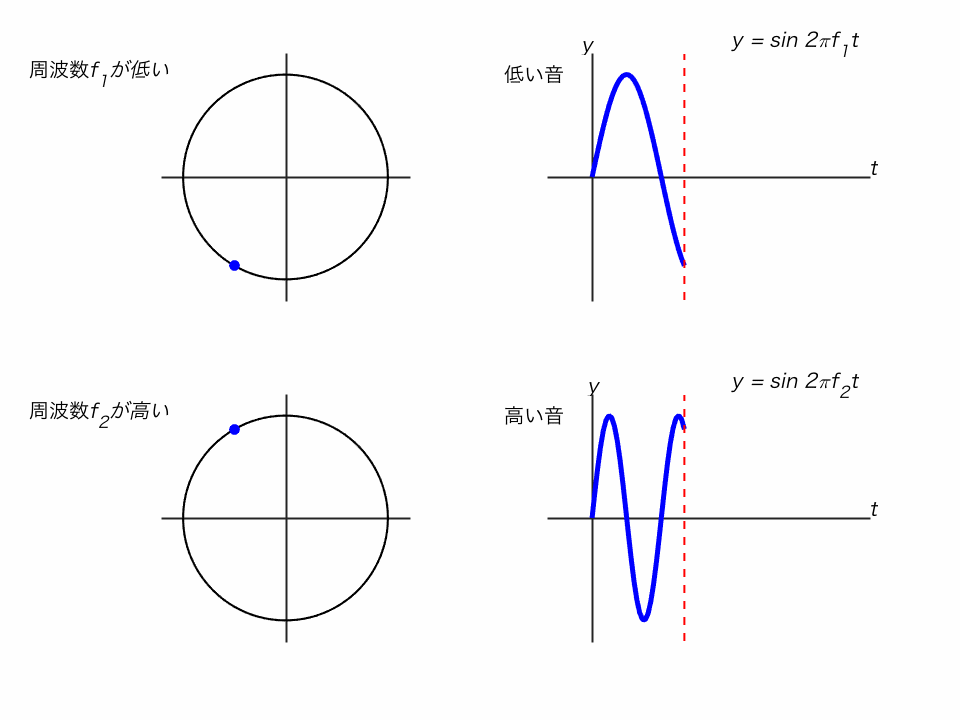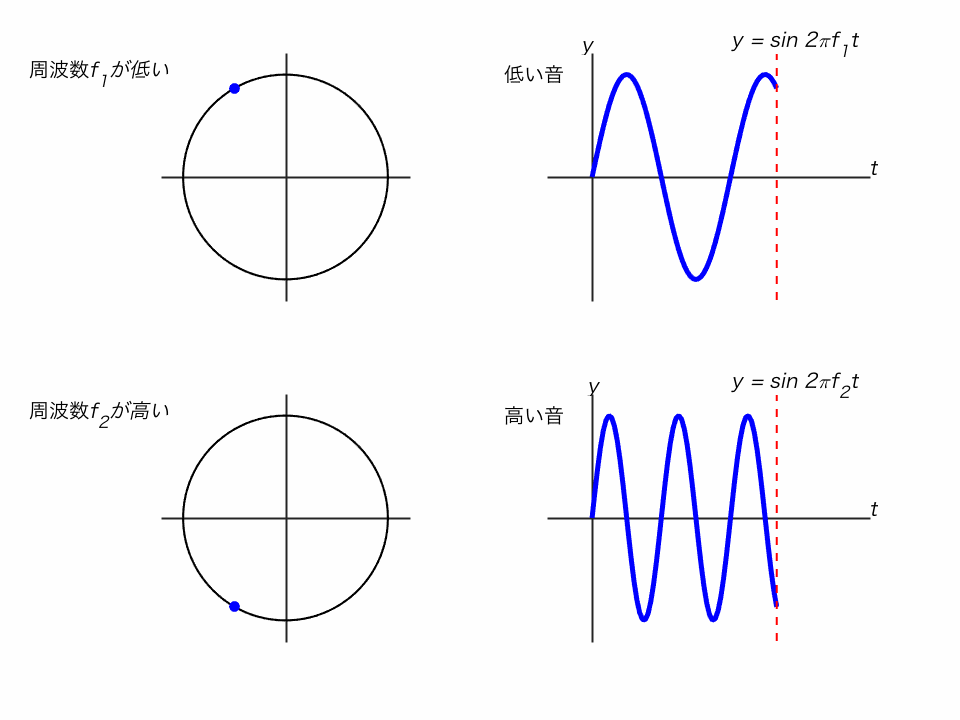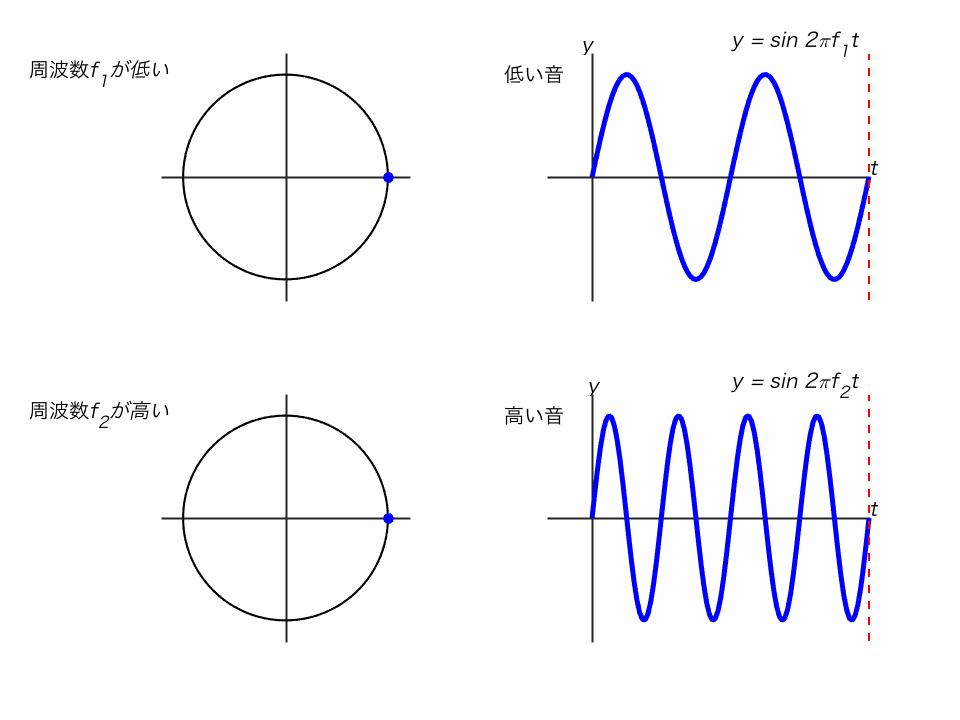
◯ 振動の振幅Aが大きいと、大きな音になります。
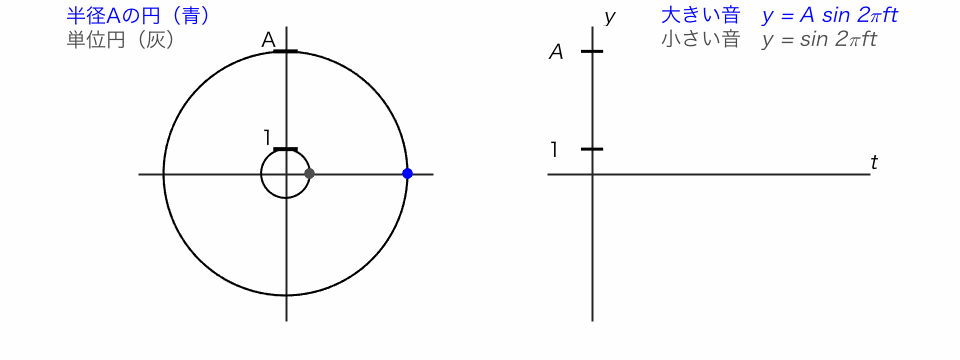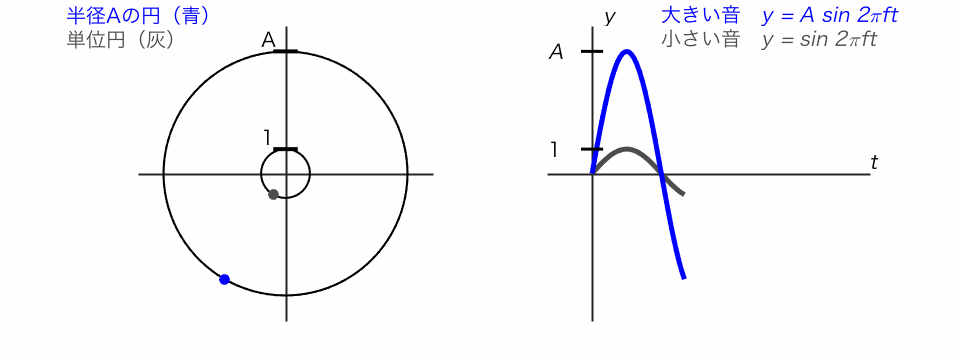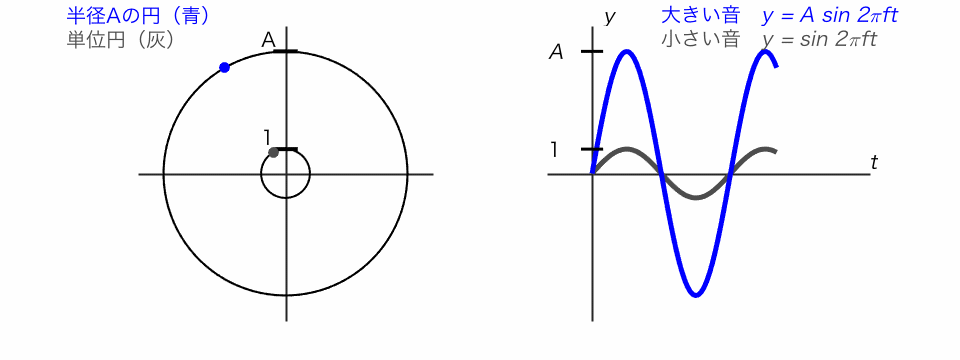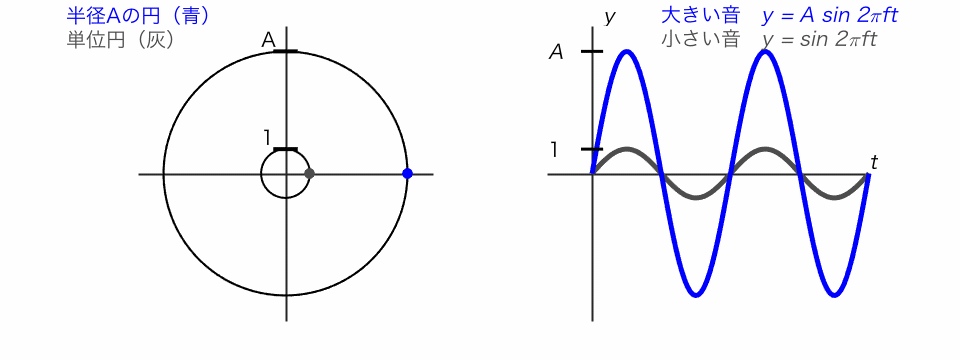
周波数 f の異なるサイン波の足し合わせが複合音です。複合音のなかでも、基本周波数の自然数倍の周波数のサイン波を足し合わせた音を調和複合音と呼びます。倍音が増えるにつれて、音色が変わっていく様子を体験しました。
調和複合音では「複数の純音」が鳴っているはずなのに、それが「ひとつの音」に聞こえるのは不思議です。またこれには個人差があり、ひとつの音に聞こえる人や、複数の音に聞こえる人がいました。このような個人差が生じるのも不思議です。また、同じ人でも、何回か聴いていると聞こえ方が変わってくることがあります。
どうしてこのようなことが起こるのか?
調和複合音は、複数の解釈が可能な曖昧さを含む音だからです。この図を見てください。真ん中の文字はBですか?13ですか?
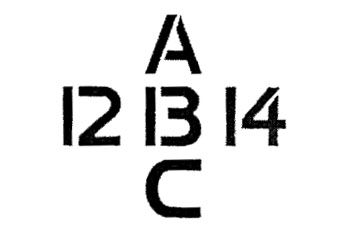
上から下に向かって読むと、ABCのB、左から右に読むと、12-13-14の13に見えます。
このように、脳は文脈に応じて「解釈」をします。調和複合音の場合も、「2つの異なる音」が鳴っているという解釈と、「倍音を含む1つの音」が鳴っている、という2つの解釈が可能です。この解釈は、ふだんは脳によって自動的に無意識に行われます。ただし、意識を集中すれば、意図的に解釈をねじ曲げることも可能な場合があります(上の図で試してみましょう)。ですから、下の受講生のコメントはとても的確です。

調和複合音の感じ方が違うことが面白いと思った。アヒルとウサギのトリックアートのように脳がどっちで行こうかと迷っている感じだった。
自然界では、単一の周波数からなる「純音」は珍しく、殆どの音が倍音を含んでいます。楽器にしろ、鐘にしろ、声にしろ、私たちが普段耳にする殆どの音は、自然数倍の倍音を含んでいます。逆にいうと、自然数倍の倍音を持つ音が、まったく異なる音源から同時に鳴るという状況は、確率的に少ないのです。
そこで脳はそのような解釈(倍音がそれぞれ個別の音であるという解釈)を、可能性の低いものとして排除しがちです。そして、1つの音源から出た1つの音として、解釈しようとするのです。
こうした事実に触れることで、最初の講義で紹介した、音とは振動が「感知されたものである」と言う定義を、徐々に実感してくるのではないでしょうか。
Q&A
今週のピックアップ
サイン関数なんて習っても意味がないと思っていた/音というものは学校で習った知識で表せられるということがわかり衝撃を受けた/数学で習うような知識は日常生活に用いることはないと思っていて、それが数学が嫌いな理由でした、などなど(多数)
サイン関数のような無味乾燥(だと思っていたものに)、意味があることに気付かされた人が多かったと思います。それはつまり、今あなたが「意味がない」と思っていることにも、意味があるかもしれないということです。
そのように考えれば、学びの姿勢は、圧倒的に変わってきます。
エントロピー増大の法則のことが気になり調べてみたところ、「物事は放っておくと乱雑・無秩序・複雑な方向に向かい、自発的に戻ることはない」という法則であることが分かった。
しかし、生物が食べ物を分解し、自分の体形を構築して維持していくというのはエントロピーが減少しているように思えた。また、そもそも生物が何も無い地球から生まれたのもエントロピーが減少しているように感じた。(工2)
素晴らしいことに気が付きましたね。その通り、生命はエントロピーを低く抑える営みです。
ただ、エントロピー増大の法則は、正確には「外部と熱のやり取りのない系」について当てはまる法則です。生物は食物として、地球は太陽光として、どちらも外からエネルギーを得て最終的には熱としてそのエネルギーを放出しています。ですから、例えば宇宙全体としてはエントロピーが増大しますが、その一部である地球を見ると局所的には、エントロピーが減少することがあってもおかしくありません。
調和複合音では、基本周波数で感じる音の高さが決まるとあったが、基本周波数の音が小さくて倍音の音が大きくてもそうなのか?(人文ほか)
よく気が付きましたね。
低い倍音が弱くて、高い倍音が強ければ、高い音に聞こえます。どの倍音も同じ程度の大きさだと、高さの感覚も曖昧になります。
講義で例に挙げられた第1倍音は440Hzで第2倍音は880Hzでしたが、この2つの音が組み合わさった音は、2つの周波数を足して1320Hzになるのですか?(人文1)
周波数はそのように足し算できません。
ピアノの高い音と低い音を同時に鳴らすと、もっと高い音が聞こえるとか平均をとって真ん中の音が聞こえる・・・なんてことはないですよね。
周波数の違う波が同時にあるということは、それはそのまま両方が同時に存在するということです。
砂糖と塩を足しても、甘みと塩味が同時に感じられるのであって、打ち消しあって味がなくなるわけではありませんね。これと、似ていると言えば似ています。
(純音が四つ重なった調和複合音のような)単純な音に対する感じ方も人や時によって異なるのだから、普段生活の中に溢れているもっと複雑な音や音楽に対して人が様々な感じ方をするのも当然なのだと思った。(人文2)
ひとつの音でさえ受け取り方がこんなにも違うのだから、LINEでのやりとりや会話の言葉選びには気を付けないといけないと思います。受け取り方が違うと分かっているだけでももっと人に優しくできそうです。(教1)
こんな単純な音ひとつでも、聞こえ方が分かれるのです。ということは、音楽や言葉もさまざまな受け取られ方があって当然ですよね。自分の受け止め方が、全てではない。
私が伝えたかった、隠れたメッセージに気づいてくれて、ありがとうございます。
音色に関しては何か単位はないのでしょうか?なかったとして、新しく単位を作って音色を数値化できないでしょうか?(工2)
音色は、音の大きさや高さのように、単一の軸で表せるものではありません。明るさ、太さ、粗さなど、様々な尺度があり、そういった尺度が一体いくつあるのかさえ分かりません。
ただ、強いて言うなら「スペクトル」がそれに近い。これは単位ではないですが、音色を客観的に表す方法のひとつです。
音色はサイン波の合成であるならば、もとの純音に戻すことは可能ですか?(農2)
複合音を、純音と純音に分解することは可能なのでしょうか?純音と純音を足すことができるなら、逆もできるような気がするのですが…。(人文3)ほか
鋭い。
できます。来週のテーマです。
教わったことの「一歩先」を自分で考えられるのは、とても良いですね。
その他
音や音楽を数式で表すのは共通の言葉で「記載」するためと聞いたが、楽譜や音符などがあるのになぜわざわざ数式で記載する必要があるのだろうと思った。(農1)
音波を数式で表す理由が、音や音楽の根源の音波を共通の記号で記載して 伝えるためだと今回の授業の始めに聞いた時には、楽譜があれば十分であると思っていました。しかし、今日の講義を聞いて、楽譜では音の3要素を的確に伝達することができないということに気づきました。 まず、大きさについては、フォルテ、メゾフォルテ、メゾピアノ、ピアノ、などの記号が書かれていますが、これは万人の共通感覚ではなく、個人差が生じてしまいます。次に、高さについては、それぞれの楽器で基準音が変わるため、一括して全楽器の楽譜を作ることができません。最後に、音色については、演奏する楽器を指定するしか方法がなく、どの楽器にも属さない曖昧な音を定義することができません。(医医1)
上の受講生の質問に、下の受講生が答えてくれています。
同じ楽譜でも、だれがどう演奏するかで、物理的な「音波」はどのようにも変わります。その「音波」を記載する方法を説明しています。それに、動物の鳴き声、ことば、雷の音、雑音、など音楽以外にもたくさんの音があることを忘れずに。今日の講義は、こうした音も射程に入れた話です。
エントロピー増大の法則
エントロピー増大の法則は初めて知った。時間が経つと波は熱になり、逆の変化はないというのが面白いと思った。(経)
聞いたことはあっても意味はわかっていなかったエントロピー増大の法則についての説明がとてもわかりやすかったです。(法)
今まで物理や化学の授業でエントロピーについて習ってきたもののいまいちイメージがしづらかったのでとてもすっきりしました。(理2)
エントロピー増大の法則は、この世のあらゆる現象の背後にある、とても重要な法則です。コーヒーが冷めるのも、水にインクを垂らすと広がるのも、脳の記憶が時間とともに失われるのも、すべてこの法則通りの現象です。
そして逆に、人の営みとは、人為的にエントロピーを減少させるのを目的としたものが多いです。
弧度法
1周が360度という値に数学的根拠がないことを初めて知った(多数)
° で表すと数学的に不自然であるからラジアンを使うということを知り、ラジアンを習った当時に疑問にすら思わなかったことに気づくことができました。(経4)
小さい頃に習ったことは、根拠などなくてもそういうものだと思い込み、自分の中で覆すことのできない常識になってしまうことがあります。怖いですよね。
このようにこの講義では、「教養」につながる「裏の意味」があちこちに潜んでいます。いちいち説明しませんので、自分で見つけてください。
度数法が数学的に不自然で、弧度法が数学的に自然だというのは聞いただけでは納得できませんでしたが、講義後に調べてみたところ、確かに国際単位系での角度の単位は「度」ではなくラジアンでした。(人文)
国際単位系(略称SI)とは、国際的に認められた単位をまとめた体系です。例えば、メートル(m)やグラム(g)はSIの単位です。一方、ローカル色の濃いヤードやポンドは違います。お米の1合、2合の合も、もちろんSIの単位ではありません。
そして、度数法の「度」も、SIの単位ではありません。
よく調べてくれました。ただ、SIに採用されいるかいないか、ということで弧度法が数学的に自然であるかどうかを判断しているとしたら、考え方としてどうでしょうか。権威に頼るのでなく、自分で考えて論理的に納得するかどうかというところで判断できると良いですね。
人為的に決めたものは自然を表すときに適合するとは限らないという例を他にも考えてみると℃と絶対温度Kの関係が該当すると思った。℃が日常的によく使うが化学や物理で使うのは絶対温度のほうであり、確かに、℃は様々な物質がある中で水という一つの物質に着目して基準を決めたが、絶対温度は振動のエネルギーが0になるところを0としたものだから色々なところで応用することができた。(医医1)
まさにそうですね。
同じものでも、測る基準を変えるだけで、全体の見通しが良くなったり悪くなったりします。
サイン関数と純音の式
日常にある音は複合音がほとんどであるにも関わらず、聴力検査で純音でテストするのはあまり意味がないように感じました。(経1)
健康診断では、1000Hzと4000Hzの純音を使います。耳鼻科の詳しい検査では、もっとたくさんの周波数の純音を使います。
純音を使う理由は、単に“音が聞こえるか”ではなく、どの高さの音が聞こえるか(聞こえないか)を検査するためです。複合音には複数の高さの音が含まれるので、この目的には合いません。
倍音と複合音と音色
合唱で和音がきれいにできたときに、誰も歌っていないはずの和音の中の最も高い音が 聞こえることがあり、合唱の世界ではそれを倍音と呼んでいたのですが、正しい呼称だったのでしょうか。(人文)
吹奏楽部でパートや、全体でチューニングをするとき綺麗にピッチがあっていると、出している音以外の音(倍音)が聞こえることがありました。これは、楽器の音が複合音のため、その音に含まれている音が聞こえてくるということでしょうか。(人文2)
音楽をやっているとハーモニーがあっているときに鳴っていない倍音が聞こえることがあります。例えば1度と5度の音が鳴ってる時に3度の音が聞こえたり、オクターブ上の3度が聞こえることがありました。個人差があるとは思いますがなぜなっていない倍音が聞こえるのか不思議に思いました。(医医1)
もともと、声や楽器の音には倍音が含まれています。みなの音程が揃い、きれいな和音になると、その倍音が足し合わさって強い音となり、聞こえやすくなります。(逆いうと、その倍音が聞こえていない状態でも、その倍音は鳴っています。)
受講者全員が全く同じ音を同じ場所で同じ時間に聞いていて条件は一緒のはずなのに聞こえている音の数が綺麗に割れていたことに驚きを感じました(教1)。
1回目の基本周波数は電子音に聞こえたが、2,3回と回を重ねるとエレクトーン、金管楽器に近い音になったと感じた。(農)
講義中に調和複合音を聞いたが、私はすべて一つの音に聞こえた。しかし周りの人は二つや三つの音に聞こえると挙手していて、感じ方の違いに面白いと思うと同時に少し奇妙さも覚えた。でも、このように人それぞれ聞こえ方が異なるのは、以前やった「音波は物理現象、音は心理現象」に密接に関係しているのかもしれないと思った。(人文)
聞こえ方の違いは解釈の違いであり、脳の個人差を反映しています。同じ人が違う状況で聞くだけでも、聞こえ方が変わることもあります。どのように聞こえたら優れているなどといった優劣はありません。単に解釈が異なる、というだけです。
最初の講義で、音は音波を感じたもの、といった意味が分かってきたのではないでしょうか。
倍音を4つ聞いたが、ソソレソの順に聞こえた。当たってますか?(工)
なぜ400-800Hzでは1オクターブ上がるのに、800-1200Hzではソからレにしか上がらないのですか?(医)、など数名
この人たちには絶対音感がありますね。このようにドレミなどの音名がわかった人は、受講生の中に、数十人いたはずです。
周波数と音楽の音の関係については、いずれ勉強します。絶対音感についても、詳しい講義があります。楽しみにしていてください。
和音と複合音の違いはなんでしょうか。(理2ほか)
鋭いところを突いてきましたね。
ひとつの音源が複数の周波数を含めば「複合音」です。複数の音源から同時に音が聞こえれば「和音」です。ただ、お気づきの通り、意地悪なケースを考え始めると、このふたつの区別は意外と難しく、何がなんだか分からなくなってきます。
ただ、「複合音」は音響学の言葉で、「和音」は音楽の言葉です。話の文脈が違うので、実際にはあまり混乱は生じません。
音色は異なる音の合成であると習いました。しかし、実際に僕が体験したことなのですがある異なる二つの楽器の音のディケイ部(コアの部分、アタックとリリースを除外した部分)を聞き比べたときどちらも同じ音に聞こえました。あれ、今日習ったことと違うなと思いました。そこで兼六館出版社の日本音楽スタジオ協会のサウンドレコーディング技術概論で調べてみました。この本には「音質について厳密に定義することは大変難しく、現在、その定義自体十分に確立されていない段階である。(中略)我々は楽器の音質の違いの判別は、音圧の変化や楽器の立ち上がり時の時間的変化などを総合的に判断しているだけに難しい判断となる。」と書いてありました。音質(音色)の違いは音の立ち上がりも関係しているのではないでしょうか。(工1)
はい、そのとおりです。倍音は、音色を決める要素のひとつですが、すべてではありません。
講義で「すべて」を伝えることは不可能です。(高校で、縦波や横波を習っても、表面波を習わないのと同じことです。)ある程度、簡略化した説明にならざるを得ません。
それを、こうして自分で考え、調べて、補っていくのが、良い勉強のあり方です。
プッシュホン式電話は音の振動数で電話番号を認識しているとあったが、なぜわざわざ音を出して認識させる必要があるのですか?番号を実際に打っているので、その打ったということを音を鳴らさずとも認識できるのではないかと思いました。(理2)
電話ですから。
電話のシステムは、ヒトに聞こえる音声を伝達するのに適した仕様になっています。そのシステムを通じて信号を送るのですから、番号であっても、音で送るのが理に適っているのです。(それ以外の方式で信号を送ると、そのための機材が、通話用とは別に必要になります。)
コナンの電話のトリックについて説明されていた。電話の音は2つの純音の組み合わせであるが、元々複合音であるはずの人間の声で、その音を本当に再現できているのか疑問に思った。(経1)
コナンの劇中ではプッシュホン式電話を二人の人間の声で行っているが、人間の声が複合音だとしたらコナンの声ともう一人の声はそれぞれ2つ以上の周波数でできている。だからぴったり作りたい周波数の波形にはならないのではないかと疑問に思った。(医保1)
プッシュホンのシステムでは、受話器に入る音から「特定の周波数の音」を検出して、番号を判断しています。他の音がまざっていても、その周波数の音が“含まれて”いれば良いのです。だからこそ、騒がしい部屋など、プッシュホン以外の音がある場合でもうまく電話がかかります。
その他
音が気圧の変化であるならば、その日の気圧によって同じ音波を出したとしても多少の音の聞こえ方の違いがあるのか疑問に思いました。(工2ほか)
音圧は気圧と比べるとかなり小さい圧力であることを学習した。このことから、なぜ小さな圧力は音として感じ取れていて、大気圧などの大きな圧力を音として感じないのか疑問に感じた。(工2)
すでに何度も何度も何度も説明してますが、音は気圧の「振動」です。気圧そのものではありません。
どういうことかというと、その地点の気圧をP[気圧]として、それが P ± α[気圧]の範囲で変動して、その±αの部分を聞いているということです。だから、気圧Pが変わっても、振動の±αの部分が同じなら、同じ音に聞こえます。
また、±α の振動は、20Hz以上、すなわち1秒に20回以上の速さでないと、聞こえません。天気によって気圧Pは変化しますが、あまりにゆっくり過ぎて、音として感知されないのです。
番外編
受講生からのおすすめアーティスト:Ichika Nito
私は最近ギタリストのIchikaNitoさんの曲をときどき聴いています。透き通った素敵な音色と繊細で惹き込まれるような演奏をされる人です。機会があればぜひ先生にも聴いていただきたいです。(人文2)
伊藤からのおすすめアーティスト:Rei
めちゃくちゃギターが上手くてカッコいい。この曲はかなりポップですが、渋い名曲もいっぱいあるので聴いてみてください。
参考図書

