講義
今回の講義では、まず、「物理世界 ≠ 心理世界」であることを実感する事から始めました。
私たちの目や耳は、物理世界の光や音を捉えますが、それを知覚して得られる心理世界、すなわち我々の脳がとらえる世界は、必ずしも、物理的世界と同じとは限りません。むしろ殆どの場合異なります。もっと言えば、同じとか異なるかを論じること自体が、意味のないことくらいに別の種類のものです。
しかし、いくら「物理世界 ≠ 心理世界」とは言っても、その対応には一定の法則があり、それを明らかにしていくのが心理学の目的のひとつです。
そのような法則の例として、ウェーバー・フェヒナーの法則を紹介しました。ピアノなどの楽器の調律や、良く耳にするデシベルという単位などが、この法則に従っていて、音や音楽の科学でも重要な法則です。
ウェーバー・フェヒナーの法則では、皆さんの苦手意識の強い対数(log)が出てきます。しかし、調律やデシベルに限らず、経済学など文系領域を含む様々な現象の理解にとって、対数の概念はとても役立ちます。数式の詳細はわからなくとも、フィーリングだけは、ぜひつかんでくれるといいなと思います。
そして対数は、この講義最終回のクライマックで、もう一回出てきます。実は、音楽の本質にせまる「情報量」というものを数式で表すことが出来て、そこに対数が出て来るのです。
Q&A
今週のピックアップ
比率を尺度にすることで相対的な量とする考えに衝撃を受けました。確かにこれなら元の何かから比べることでそこに量の概念を持ち込むことが出来ると思いました。(教)
1メートルとか、1グラムとか、1秒とか、そういう物理世界の絶対量の単位は、心のなかの感覚の尺度としては使えません。あなたと私で、その量に対する感覚が等しいことが、保証できないからです。
だから感覚量は、ある共通の物理量(例えば1000Hzの20μPaの音)に対する「個人の感覚量そのもの」を基準として、比率でとらえます。
比率で考えるということは、比をとるのですから、物理学的な意味での単位(次元)は消滅することに注意しましょう。
物理量が等比数列的に増えると感覚量は等差数列的に増えるということで、今回は聴覚がメインでしたが、人間の五感はすべてこの法則に従っているのか疑問に思い、なにかいい方法はないかと家の中を探し回りました。そこで、大量の野菜ジュースの缶を一本ずつトレイに乗せて持ってみたのですが、確かに缶の本数が倍になったときにより重さを感じました。(物理量と感覚量の知識を得たうえで行ったのも大きな要因だと思いますが…)その後も32本まで乗せてみて一本ずつではなく倍ずつ乗せてみたりしたのですが、こんなに簡単なことでもやはり感覚を数値化したり言語化することの難しさも感じました。(人文1)
すぐに実験をした行動力が素晴らしいですね。だからこそ、この受講生は実感をもって気づいたのですが、感覚の定量化とは、実は非常に難しいものです。
半分のピッチや、半分のラウドネスとは、いったいどんなものか? そう聞かれると、講義で分かったつもりになっていたものが、途端に分からなくなってきませんか? 感覚量とは、そのような危うさを持った概念です。
漢字の「大」と「人」と「銀閣寺」の実験ですが、例えば「人」を黒、「銀閣寺」と「大」をどぎつい色(ショッキングピンクとか)に変えたり、各文字の彩度を調節して視認しやすくしても文字は消えてしまうのでしょうか。気になりました。(工1)
「大」の字や「銀閣寺」の文字が見えなくなりましたが、例えば周りにあった「人」の字をなくしてもっとシンプルなものにしたら見えるのでしょうか。(教1)
講義中「大」や「銀閣寺」が見えなくなるという実験をしたが、どのような条件で見えなくなるのか疑問に思った。この現象に興味を持ち、自分でも背景を白紙のまま同様の検証を行ったが上手くいかなかったため、周りにごちゃごちゃとしたもの(講義中の実験でいう「人」の文字)が必要要素のひとつと考えた。(工1)
最後の受講生。自分ですぐに実験をした行動力が素晴らしい。
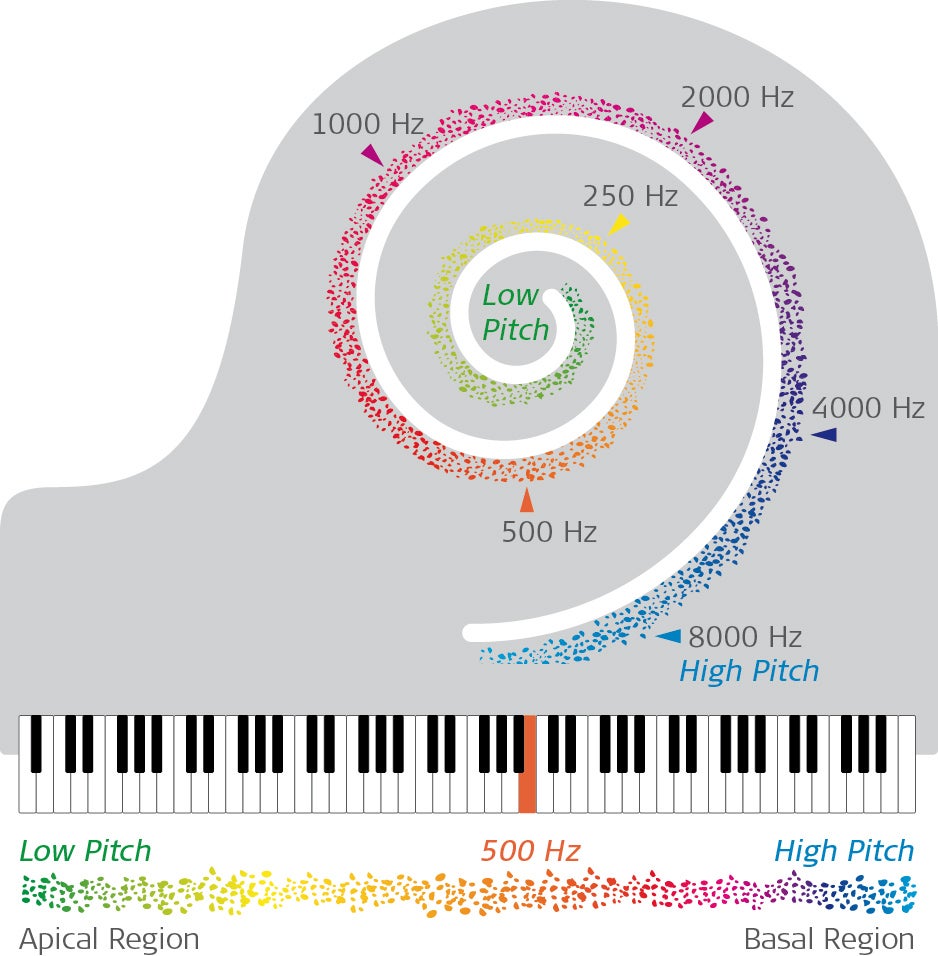
聴覚に関して、フーリエ変換を行い物理量の対数をとるような器官が蝸牛であると考えることが出来るのではないかと思った。(工2)
すごい。よく気付きましたね。蝸牛における周波数の目盛りが対数になっています。基底膜上の周波数の分布自体が対数なのです。
毎回レポートを書くのは正直大変ですが、このおかげで、他の授業のレポートが書きやすくなり、最近良い評価もいただけました。この講義で得ることができているのは知識だけではないと心から感じます。これからも頑張ります。(農1)
No Pain, No Gainですね! 毎週のレポートは、いわば、脳の筋トレです。きちんとやれば、必ず身になります。
これまでの講義後のレポートでは、必死に質問を考えて入力していました。その結果内容の薄い質問となり、後になってよく考えると講義の内容の中に答えがあるじゃないかというものばかり送信していました。今日も先程まで必死に疑問や質問がないか考えていましたが、疑問や質問は考えるものでなく、何かを理解しようとする過程で自然と頭に浮かんでくるものなのではないかとふと思いました。(人文1)
素晴らしいことに気が付きましたね!
そのほか
「物理世界≠心理世界」
物理を学んでいるので、脳が知覚している世界が、実は違う世界だということを意識したことがなかったが、そういう視点も必要だなと思った。心理学をなめてました(理)
心理学という学問のイメージが変わった人も多かったことでしょう。
大文字を凝視したときに銀閣寺が見えなくなりましたが、見えるはずのものが見えなくなるのはかなり不便じゃないですか。(教)
脳の処理能力は有限です。無限の解像度で何もかも詳しく見ることはできません・
だから、ある点を集中してしっかり見ると、それ以外のところを見ることを妥協しないといけません。そこで脳はどうするかというと、周りにたくさん「人」があるのだからどうせ全部「人」だろうと、推測をするのです。
これを不便と取る気持ちも分かりますが、私は逆に、この柔軟性が素晴らしいと思います。
有限でしかない脳処理の資源を、自由自在に配分し、時には一点にフォーカスし、時には全体を広く見渡すことで、状況に応じた必要な情報を得られるのですから。
京都の大文字の実験をして、歩きスマホの危険性がよく分かった。今まで、歩くときに前をチラチラ見ればそれほど危険だとは思っていなかったが、そういうことではなく、画面に集中してしまうことがそもそも問題なのだとわかった。(医保)
ほんとにそうです。
ウェーバー・フェヒナーの法則
ピアノの音階が等比数列で上がっているなんて初めて知りました。私の感覚では、どちらかというと等差数列のような気がするのに…(医保)
それがまさに、ウェーバー・フェヒナーの法則です!! (^^)
曖昧なものである心理量が数式で表せることが不思議(経、他多数)/心理量については、個人差があるので、そのように数式ではあらわせないのではないでしょうか?(教育)
ウェーバー・フェヒナーの法則はどのように立証したのかが気になる。感覚量には誤差があると思うので、その法則に至るまでが難しそうだ。それともただの思考実験なのだろうか。(人文1)
ウェーバー・フェヒナーの法則では周波数のような物理量を式に入れると、感覚量の数値がひとつだけ決まる、というようなイメージを持ったかもしれませんが、そうは言っていません。物理量の増え方に対して、どのように感覚量が増えるか、という増え方の対応関係について述べただけです。
そしてその対応関係は、物理量がどのくらい増えたから増えたことに気づいたかといった実験を多くの被験者にやってもらい、その平均を取ることで明らかにしていきます。
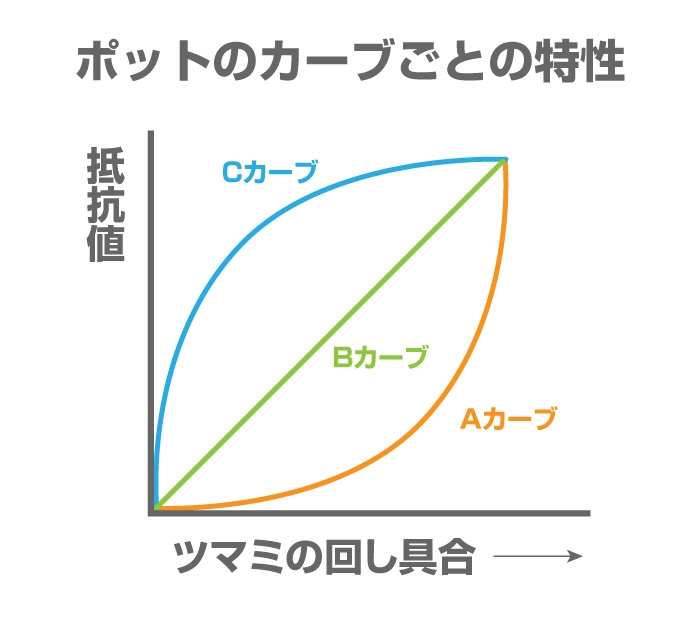
ウェーバー・フェヒナーの法則を聴いたとき、Cカーブ(reverse-log)の変化をする可変抵抗器(ポット)が少ない理由が分かり納得した。(工)
つまみを回してラジオなどのボリュームを上げるとき、回転角に比例するように音量を大きくするには、音圧(物理量)は指数関数的に増えるようにしないといけません。それを実現するのが、Aカーブの可変抵抗器です。

味の感じ方も指数関数的な増え方をするということですか?五感それぞれによって指数関数の上がり方にも急であったり緩やかであったり違いはあるのでしょうか?(人文2)
感覚によっては指数関数的(対数的)ではないものもあります。例えば、皮膚に与える電気ショックは、ピッチやラウドネスとは逆に、電流をちょっと増やすと急激に痛みが強くなります。危険を回避するには合理的なしくみです。
音の高さや大きさは、対数関数と関係性があるということを知りました。そこで、音色を対数関数で表すことはできるのか疑問に思いました。(農2)
音色は、重さや音の高さといった1次元の感覚とは違って、多次元の感覚です。そのため、ひとつの量としては表せません。
対数のグラフを見て、経済で学ぶ効用関数に似ていると思った。(経3)
そうですね。
経済学には限界効用逓減の法則というのがあり、これは、ある商品やサービスを同じ量だけ増やしていっても、そこから得られる心理的効果は、次第に減っていくということです。「1万円をあげる」の話と似ていますね。(厳密には、これは必ずしも対数になるとは限らないのですが、グラフで表すと上に凸になのは同じです。)
感覚量が物理量の対数に比例することがどのように生存に有利に働くかが不思議で、疑問に思った。(医医1)
小さいものから大きいものまで広い範囲の刺激を、狭い範囲に”圧縮”して感覚として受け取れるのがメリットです。
メトロノームの目盛も、2刻み、3刻み、4刻み、6刻み、8刻みと等比数列的なのはなぜなのだろうか。(工2)
高校で共通テスト対策をしているときに星の等級と対数に関する問題があった.当時はなぜこのような等級の決め方をしたのか不思議だったが,今日の講義を聞いて人間が感じる明るさの違いは音のピッチと同様に等差数列的ではなく等比数列的なものであるからだとわかった.星の等級にも負の数があることは星の等級と音のピッチは同じような決め方をしていることに由来する類似点であることに気づくことができた.(工1)
Microsoft Wordのフォントサイズは,小さいサイズから大きいサイズまで幅広く設定できるようになっていますが.よく見てみると,最初は小刻みなのにいずれ24pt,30pt,36pt,48pt,60ptと,突然倍率が大きくなっています.こうなっているのは,フォントサイズの60ptと61ptを比べたところで,ヒトにはその違いが分からないからだということを理解しました.(工3)
他にも対数の関係になっているものがあるのか気になり調べてみました。すると、音の他にも地震のマグニチュードの例が出てきました。マグニチュードとは地震のエネルギーを1000を平方根の底とし対数で表した数値だそうです。地震のエネルギーが約32倍になって、マグニチュードが1増え、地震のエネルギーが約1000倍になってようやくマグニチュードが2増えるといったように、対数の関係になっている。
みなさん良く気がつきました!
星の明るさは、5等級あがると100倍明るくなるように比率で決められています。ですので、1等級分の明るさの変化は、100の5乗根(5乗すると100になる数)で、2.512…倍です。
このような例はたくさんあり、化学のpHや地震のマグニチュードも、同じ仕組みの単位で、メトロノームの目盛も似た現象ですね。
対数(log)
高校生の時の私は、logって何に使うんだ?と思いながら、必死に規則を覚えただけでしたが今日の講義を聞いて、logを使うと一気にわかりやすくなるから、使うと便利だということで使われてきたんだということがわかりました。それを知ってからlogという文字を見るとなんだか感動すらしてきました。(人文ほか多数)
対数は重要です。この世には、比で変化する量がたくさんありますが、対数は「比で変化する量を扱うのに自然」な概念だからです。
デシベル
一般的なオーディオは0を基準にして正の方向に増加させるような形態をとっていましたが、なぜ、高級なオーディオになると負の方向に減少させるような形態をとるのでしょうか。音を流すといった目的は同じなのに基準を変える理由が分かりません。(農)
スピーカーの最大音量を0dBにして、それより小さい音をマイナスで表す意図・利点は分からなかった。(法3)
0と-∞で表記されているオーディオ機器があり、普通に考えればつまみの方向的にも-∞より0の方が大きそうだと気付くはずですが、∞と書いてあると不安になり、違和感とただならぬ胸騒ぎを感じつつ0dBで再生してしまった結果頭が吹っ飛ぶかと思いました。どうしてそんな分かりにくい表記をするんだ!許せない!と思った記憶があります。しかし、CDなどの記録媒体に音を記録するにあたって、必ず上限というものが存在するので、明確に最大値であることを示す基準としては0dBが最適なのかなと思い、少しだけ腑に落ちた気がします。(医医1)
どのようなオーディオ機器も最小音量は無音で同じですが、最大音量は機器によってそれぞれバラバラですよね。だから、機器ごとにその最大値を基準にするのです。
オーディオ機器を「作る」プロの立場からすると、音量というのは、最大値を基準に設計して、そこから(電気抵抗を増やすなどして)小さくしていくもの、という見方になります。一般人の発想のように「無音から大きくする」のではなく、もともと大きいものをアッテネーター(減衰器)で小さくするという発想です。
ですから、最大音量をゼロdB(=基準)とする、あるいは(音割れを防ぐために)推奨される最大音量をゼロdBとする、というのが理にかなっています。
ただ、これがいかに自然で正しいとは言え、一般の人には意味が通じませんよね。だから、そちらの事情に合わせて、やさしい気持ちで、無音をゼロと表示するような機器が多いのです。一方、素人が手を出さない高額商品なら、購入者の意識レベルも高いので”本来の表示”で意味が通じるだろうということです。
その他
京都五山の送り火を表した図で、ある一点に注目すると周りにあるほかの文字が消えて見えなくなり、赤い文字すらも全く存在を感じなくなるのを実感して、驚きとともに少し恐怖を感じました。この現象は、自分や属する集団の考えが絶対的に正しいと無意識に思い込み周りが見えなくなってしまうことや、現代ではSNSで自分が興味のある情報だけを選んで深く知ることができるために関心がないものは全く見えなくなってしまうことに似ているなと感じました。(人文1)
まさに、初回の講義で話した「教養」に通じる話ですよね。
あの犬の絵を見て「ひょっとしたら2匹なんじゃないか?」と疑えるくらいに頭を柔軟にするためにできること(普段の過ごし方や考え方)があれば知りたいと思った。(ひらめき力を鍛える問題集などもありますが、私はひらめくかひらめかないかは運によるところも大きいと思っていて、あまり効果がないのではないかと考えています……。)(人文1)
ひらめきを支えるのは、経験の豊かさではないでしょうか。例えばあなたも、次にあの絵を見たら、二匹かも?と想像するでしょう。何でもどんよくに経験して、想像の可能性の幅を広げていきましょう。
なぜ、日本は心理学を文系分野で学ぶことができるのでしょうか。心理学は心の科学と聞き、理系分野の学問なのではないかと疑問に思いました。(人文)
心理学は、文系の学問だと思っていましたが、今日の講義で、理系の学問ではないかと疑問に思いました。実際はどちらなのでしょうか。(教)
そもそも、理系・文系という分け方が、乱暴でおかしいのです。有害だとさえ思います。そんな垣根なんて、そもそもなく、全てが繋がっているからです。このような分け方をするのは、日本だけではないでしょうか(そこまで世界のことを知らないので、多分、の話ですが)。
ですから、その無用で有害な枠組を、せめてみなさんの頭の中だけでも、ぶっ壊すような授業を心がけています。
「数学って何のために勉強するのか、将来使わないだろ」という意見があり私もそう考えていた。しかし、前の講義での音の波は三角関数のグラフで表せるということや、今回の講義での心理量を対数を用いて表すことなど、数学を使う場面は思っていたよりも多いと分かった。今まで苦しんで数学を勉強してきた意味が分かった気がする。(医保)
実際に対数を習う高校生時代には、私はなんのために対数を学んでいるのかよくわかっていませんでした。高校を卒業するためだと思って頑張っていました。なぜ、高校の数学は、対数などの数学の専門的なものが何に役立つかを教えてくれないのでしょうか。少なくとも、何に役立つかの例があるともっと数学を頑張る生徒が増えるのではと思いました。(人文)
中学や高校で教えられていることで、無駄なことなど何ひとつありません。無駄だと感じてしまうのは、単に自分が、無知なだけです。(という見方をするのが、自分の為になります。)
ただ、私が数学を勉強したのは、ただ純粋にそれが楽しかったからで、役に立つかどうかなんて発想は、そもそもありませんでした。数学を教える先生も、どちらかと言えば、そういう人種なのかもしれません。
ただ、それは少数派ですよね。
だから、多数派の、決して数学が面白いと思えない皆さんに数学を学ぶ意義を教えるには、教える側の意識改革が必要かもしれません。この講義は、そうした試みです。
先生はどうやって色々な分野に精通して、音楽に繋げているのですか?何かきっかけがあるのでしょうか?一つの分野を掘り下げることも大変なことだと思いますが、色々な分野を浅く広くではなく、深く理解していることが凄いと思いました。(理)
「自分で考える」ということに尽きます。ググるのでなく、考えるのです。いや、ググりもしますが、さらにその何倍も何倍も考えるのです。
この講義で話している内容の99%は独学です。すなわち、誰かに講義で教えてもらったのではなく、教科書などで自分で勉強したことの再構成です。知識は色々なところから集めてきますから、断片的なパーツでしかありません。そのパーツを体系的につないでいくのが、「自分で考える」という作業です。
単に「知っている」のと「理解している」の違いは、この再構成の作業を、苦労して自分でするかどうかの差です。No pain no gainを思い出しましょう。
以前の授業で音の大きさについて聞いた時には、デシベルというものが何か完全に理解した気になっていました。しかし、今日、デシベルについて一番大切なことを隠して説明されていたということを知りました(工2)
この講義にはたくさんの伏線が張り巡らされています。チラ見せだけして、あえて、説明せずに残していることがあるのです。
これから、次々と伏線の回収作業に入っていきます。
音の高さについての用語の箇所で、ピッチとは感じる音の高さだと学びましたが、私たちは何かのペースを表現するとき、「ピッチ」という言葉を使うと思います。この違いには何か関係があるのか、疑問に思いました。(教)
他にも、サッカーのフィールド、野球の投球、飛行機などの機首の傾き、ビールを入れる容器(ピッチャー)、石油などから精製される黒い樹脂・・・といった、たくさんの意味があります。
共通項がはっきりせず、なぜ同じ単語なのか、私にはさっぱりわかりません。
答えがわかった人は、教えて下さい。
