講義
今日の第1の目標は、純音(サイン波)の式を完成させることでした。前回、サイン波は数式で、y(t) = A sin 2πft と表せると習いましたが、実はこれは不完全。初期位相(+α)という概念を導入し、このように式が拡張されました。
y(t) = A sin (2πft + α)
初期位相とは、時刻ゼロ(t=0)の時の位相です。下の図は、青い点の初期位相が0、赤い点の初期位相がπ/2で、よーいどんで同じ周波数で回転を始める様子を表しています。
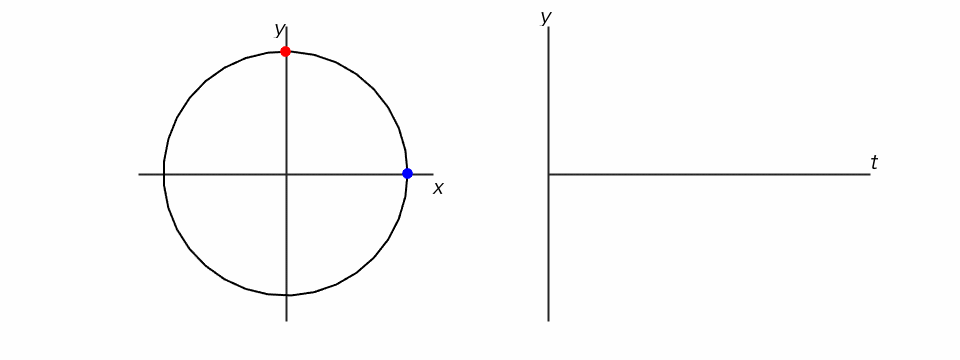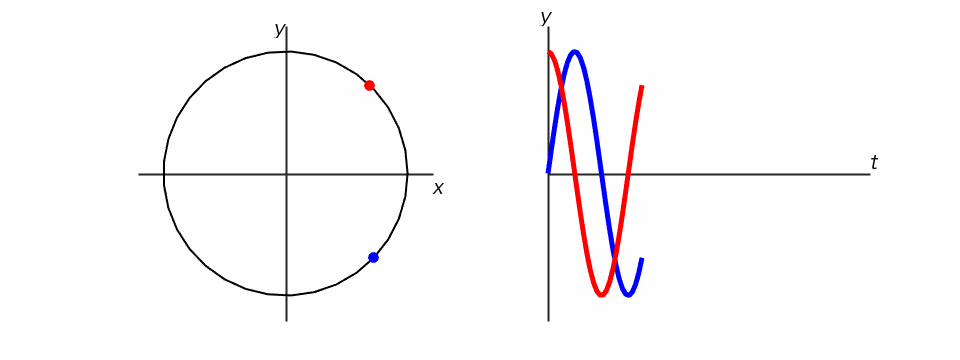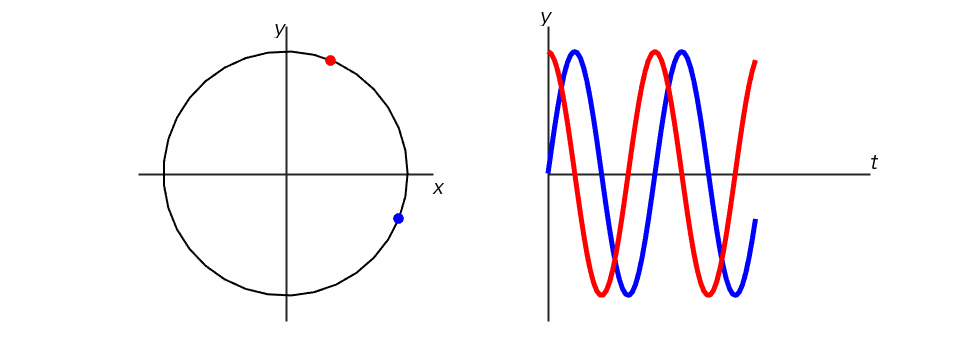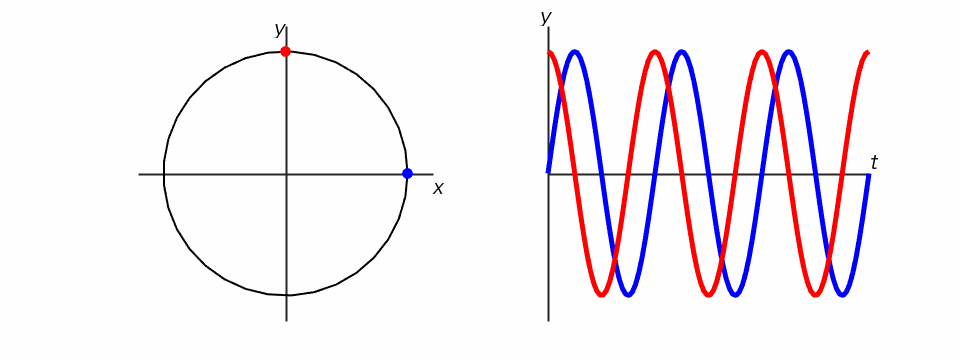
この時のそれぞれの点のy座標をグラフにすると、青い点の軌跡は先週習ったサイン波になりますが、赤い点の軌跡は、実は、コサイン関数と同じになります。つまり、コサインはサインを横にずらしただけ、ということがわかります。
そしてメインの目標は、フーリエ変換を概念としてつかみ、スペクトルとは何であるかを把握することでした。
式は理解しなくて良いです。パソコンの内部の仕組みを知るのと、パソコンが何をできるのかを知るのは、別のことです。フーリエ変換の数学は難しいですが、”それが何をしているか”という意味だけなら、それほど難しくありません。
音を様々な周波数のサイン波の和に分解するのがフーリエ変換で、その結果として得られる音の成分表がスペクトルです。ここまで理解できれば十分です。
フーリエ変換の数学的な仕組みを知りたい人は、参考図書「フーリエの冒険」で勉強しましょう。幾何学空間でxyz軸を直交基底に取るように、「関数空間では、様々な周波数のサイン関数を直交基底に取る」こと、そしてフーリエ変換は「その基底への射影を計算している」のだという感動の世界観が、あなたを待っています(この講義のレベルを遥かに超越した話です。)

文系でもわかるフーリエ変換ということでしたが、私にはよく分かりませんでした。
・・・しくしく😥
来週からは簡単(?)ですので安心してください!
おまけ:「タンジェント波」というのはあるのでしょうか?
講義で質問しましたが、答えは分かりましたか?

多くの人が正解してくれました。
タンジェントのグラフを描くとわかりますが、これは所々で無限大に発散します。一方、音にせよ何にせよ、波は「現実世界の物理現象」ですから、その振幅が無限大になることはあり得ません。ですから、「タンジェント波」は存在しません。値が不連続なところがあるのでそのような波は存在しない、値が定義できないところがあるので存在しない、という回答も正解です。
数学と物理学のギャップについて考える問題でした。
Q&Aコーナー
今週のピックアップ
すべての音は純音の和に分解できるとのことだったが、例に出てきたのこぎり波のようなカックンとした波形は、いくら波を足し合わせても”近づく”だけであって厳密には再現できないのではないか。すなわち、波を足し合わせて「近似できる」という認識でよいのか。(理2)
そうです。途中でやめれば「近似」です。しかし、無限に続ければ、近似ではなくイコールです。
倍音の波は曲線なのに、その足し合わせで矩形波の中の直線を表すことが可能なのでしょうか。丸は四角にならないので、最終的にサイン波が本当に矩形波になるのか疑問です。(法、医など)
周波数の高いサイン関数は、曲線が急激に立ち上がり、急激に下がります。この考えを進めると、周波数が無限に高いサイン関数は、立ち上がりが直角になることがわかります。
波形がカクカクしているということは、そういう高い周波数の音を含むということです。
直角のような波形を作るのに、周波数を高くしていたが、人間の聞ける音の高さには限界があるのだから、ある一定以上は音として成り立たず、あの形の音は正確には聞こえないのではないか?(経)
フーリエ変換について、目的の波形に近づけるために、音圧が小さく周波数の高い音を無限に足していく手法をとっていましたが、人間の耳に聞き取れる最小音圧や最高周波数がある以上、感覚的にはある段階で変化していないように聞こえるのでしょうか。(工3)
鋭い。その通りです。よくごまかしに気づきましたね。
質問が来てしまったので本当のことをいうと、まず、厳密な矩形波は、そもそも物理学的に実現不可能です。直角に立ち上がる波形の音など、実際にはあり得ません。瞬間的に(つまり所要時間0秒で)気圧が変化することはあり得ないからです。
そして、上の質問をした学生が気付いてくれたように、知覚の制限もあります。
だから、物理的に可能な範囲で限りなく矩形波に近い音波を聞いたとしても、その知覚は、人間の能力の限界によって制限されたものになります。ずっと高い音まで聞こえるコウモリは、ヒトとは違うふうに、矩形波を聞いているでしょうね。
(ホワイトノイズがあるなら)ブラックノイズと呼ぶようなノイズは存在するのか、あるとしたらどのようなスペクトルが集まった状態をそう呼ぶのか疑問に思った。(工2)
連想から、疑問が生まれる。素敵です。その調子で。そして可能なら、もう一歩踏み込んで、自分で答えを見つけ出せるといいですね
黒とは、光がないことです。ですから、音に例えるなら無音ということになるでしょう。
水も食料も無限ではないですし、時間だって制限があります。この世界は有限なことに満たされていると思うのですが…。(農1)
二分法のパラドックスについての知識が無かったので調べてみました。どうやら、目的までの距離を半分ずつ進んでいくと永遠に(無限に)到達できないというパラドックスらしいです。この話を聞いて僕が気付いたのは、無限は考えなければ見えないということです。何も考えずに進めば、その人は目的地に着くでしょう。しかし、二分割するという考えを持ってしまったがゆえに無限を認識してしまいました。無限という特別に感じるものが自分の認識一つで現れる。世界を変えるというのはもしかしたら行為ではなく認識なのかもしれません。(工1)
これまで「無限」と言われると宇宙空間などの限りなく広がっていくものを連想していました。しかし、今日の講義で弓矢の矢と的までの距離もある意味無限だという話を聞いて、「無限」とは自分で数えることのできない最も小さな数であるとも言えると思いました。(保)
たった1cmの有限の長さの線分にも、無限個の点があります。たった1秒間の時間にも、無限個の瞬間があります。無限ファンとして、めまいがするほど楽しい想像です。
このように、無限は大きいものばかりではありません。小さい方向への無限もあります。ただ、無限に小さいという概念を、最後の学生のように「もっとも小さい数」と言ってしまっては間違いなんです。
なぜなら、「もっとも小さい数 = a 」があったとしても、それよりさらに小さい数 b を考えることができるので、a がもっとも小さいという仮定に反してしまい、矛盾が生じるからです(背理法による証明)。まったく同じ理由で、「もっとも大きい数」もありません。
奥が深いですよね。
急に気圧が変化することにより、音の出だしにプチッという音が入るということでしたが、ノコギリ波や短形波では波中に急激な気圧の変化があるのに、そのような音がしないのは何故でしょうか(工1)
周期のある波について凸凹のような波形の音を聞きましたが、それも気圧の変化が滑らかでなく激しい部分があったと思います。なのでブチブチという音の続に聞こえるかと思いましたが、そう感じませんでした。(工3)
とても良い質問!!
「コサイン波」で”プチッ”となるのは最初の一回だけですが、ノコギリ波や短形波では、その”プチッ”が1秒間に何百回や何千回という速さで繰り返されます。高速すぎるので、もはやひとつひとつの”プチッ”を個別のものとして認識できません。すると、あのような音色に感じられるのです。
そのほか
初期位相とコサイン
再生中の音を止めるとスピーカーがプチと鳴ること対して、当たり前の事に思っていたけれど、鳴る理由が今日初めてわかりました。プチという音の原因が初期位相だと初めて知りました。などなど。(多数)
無音、つまり振幅がゼロの状態から、突然(不連続に階段状に)大きな音を出そうとすると、プチという雑音が入ります。音が出ている状態から、急に無音にする場合も同様です。
これは、極めて短時間に振幅が急に変化することで、意図していない音(すなわち雑音)が出てしまう、ということです。この高い周波数の雑音が、プチ、の正体です。
これを出さないようにするには、音の立ち上がりや終わりを、滑らかにフェードインやフェードアウトする必要があります。一部のオーディオ再生機や再生ソフトは、このプチを鳴らさないために、音を自動でフェードインやフェードアウトさせる機能がついているものも多いですよ。私が講義で実験をする上では、ちょっと迷惑な機能です・・・
sinの後にcosができたと知り、sin・cosの語源がきになったので調べてみました。「sin」という記号は、「sinusoid(正弦曲線)」が由来で、sinusoidは「sinus」(曲がり、湾曲、湾)と「oid」(のような、に似た)と言う意味があるるそうです。また、1583年にデンマークの数学者であるトーマス・フィンケが著書で、「sin.」と短縮を示す意味での「.」付きで使用したのが、最初の三角関数の略語の使用であるとされているそうです。「cos」という記号は、co-sineの略語であり、「sin」に、補足的・補完的(complementary)の意味を有する接頭辞「co」を付したもので、「余角(complementary angle)」(角度θに対する(90°-θ))に対する「sin」との意味合いを有しているそうです。由来を聞くと、sinの後にcosができたことがよくわかりました。(農1)
解説ありがとうございます。
非調和複合音
非調和複合音を聞いてみて,先週聞いた調和複合音に比べて少し不快な感じがしました.実際には4つの波が重なり合っているのにすべての音を聞き分けることがなかなか難しいこと,また,人によって聞こえ方が違うのはとても興味深かったです.(理ほか)
非調和複合音の部分で2つの音が組み合わさっていたときはとても不快に思ったのですが音が多くなればなるほど一つの音になっていくという話を聞いて考えたことがあります。例えば、歌が下手な方がカラオケで歌っていたとします。音がずれていてあまり心地いい音ではありませんよね。しかし、合唱などで歌が下手な方がいたとしてもあまり目立たず、不快な気持ちにはあまりならないと思います。これはこの重なると一つの音のように聞こえるようになるためでしょうか。(工)
整数倍でない倍音(上音)は、小さい振幅で少しだけ含まれる分には、耳に違和感なく、むしろ素敵な音に聞こえることも多々あります。しかし、講義で聞いたもらった倍音は振幅が大きかったので、不快に聞こえた人が多かったことでしょう。
高さがぴったり合っていない音や声は、その数が2個や3個だとずれているのが目立って違和感が強いですが、合わないものもあまり多くなってくると、逆に全体がひとつにブレンドして、いい感じに聞こえるくることがあります。合唱なんか、その例ですね。
これは、複数の音が鳴っているととらえるのか、(たくさんの成分を持つ)ひとつの音ととらえるかの違いです。隠し味と称してカレーに色々と混ぜ込むと、なんだか全体で美味しくなる、みたいな感じです。
フーリエ変換
別の授業でフーリエ変換を習いました。しかしそこではフーリエ変換の意味や、どんなことができるのかなどの説明はなく、ただただつらい計算やプログラミングでした。そのこともあって今回の授業はとてもすっきりしました。(工)
いつも機械的に計算をしているフーリエ変換はこんなにもすごいものだったのかと改めて認識しました。(工)
フーリエ変換は勉強したことがある人も、実はあんまり意味がわかっていないことが本当に多いのですが、私にはそれがとても不思議です。意味が分からないまま計算だけして、何の意味があるのでしょう? この問いかけは、あなた自身へ向けたものでもあるし、あなたにフーリエ変換を教えた先生に向けたものでもあります。
難しそうに見えるものも、意味がわかってしまえば、じつは案外簡単なものです。ぜひ、「意味がわかる」努力をしましょう!
フーリエ変換は、素因数分解のようだ(人文1)
すばらしい。本質をつかみましたね。
これが理系学部でなく、人文学部の学生なのも嬉しいです。
こんな関数もsin波を足したもので表せますか?(工)

表せます!フーリエ変換は、すごいんです(笑)。
フーリエ変換では、y軸の負の方向に進む時にx軸に対しても負の方向に進むような波も作れるのでしょうか?(工)
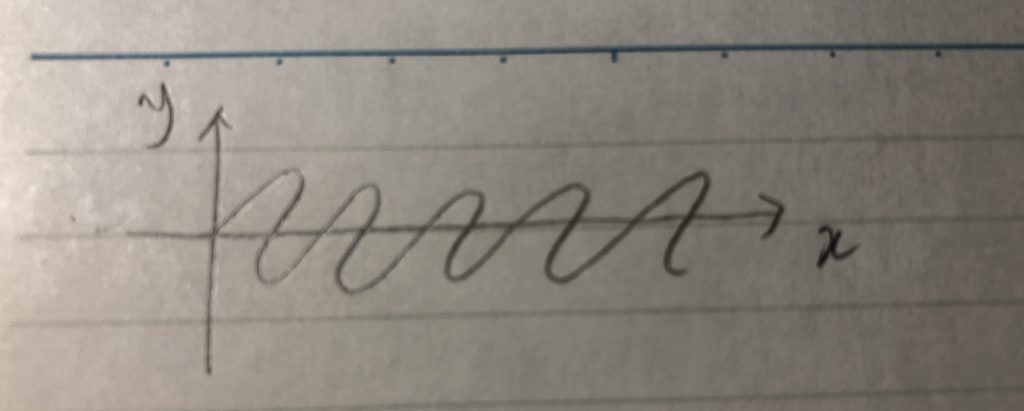
しかし、これはどうでしょう。
実は、これはフーリエ変換できません。というより、このような波は、そもそもあり得ません。ある一つの時間に、異なる状態(気圧y)が二つ以上存在するグラフだからです。音で言えば、ある瞬間に、複数の気圧状態を同時に取るなんていうことが、あるはずがありません。
関数の「定義」を知っていますか?
あるxについて、対応する値がひとつだけ定まるのが関数です。サインもコサインもタンジェントも全て関数ですが、あなたのグラフは関数ではありません。一つのxに複数の値が対応するからです。
フーリエ変換は「関数」に適用できるのです(細かくいえば他の条件もあります)。
無限、アキレスと亀、五条悟(呪術廻戦)
足していくと絶対2にならないのは最初理解できなかったが、木の例で理解できて、思わず声を上げてしまった(法)
無限の話が面白かった。最初は1+1/2+1/4+…がどれだけ足しても2にならないというのは訳が分からなかったが、木の例えを聞いて理解することができた。無限に数を足していっているのに、その和には限界があるというのは驚きだった。(人文)
無限に足しても和が有限にしかならないというのは、無限の不思議に触れる最初の一歩ですね。そして実は、これがわかれば、アキレスと亀のパラドクスも、わかるはずなのですが・・・
アキレスが亀を追い越すまでの距離を無限に細かく切っているだけであり、人間が無限に対する直感と論理のからくる認知のずれを利用した面白い話だと思いました。(理)
「無限の時間をかけても追いつけない」ではなくて「無限に話を終わらせないことができる」ということなのでは・・・?(経)
授業後冷静に考えてみると、追い越す瞬間までの時間を無限に刻んであたかも追いつけないかのように感じさせられていただけだと気づきました。(農)
私はアキレスのパラドックスは、アキレスが前に亀がいた位置にいくまでの”時間”が無限に小さくなっていくことがこのパラドックスを生み出している原因だと考えている。アキレスと亀は、アキレスが亀に追いつくまでの瞬間を無限に細かく描写しているだけなのだと考えている。(教4)
皆さん鋭い。
追いつくまでの時間は、もちろん有限です。しかし、その有限な時間には、無限の数の「瞬間」からなりなっています。(1cmの線分に無限の点があるのと同じです。)
今日初めて五条先生の言っている「無限」の意味を理解できました。すごく感動しました。触れられないってどういうこと…?先生と敵の間に何かあるの?と思っていました。(理)
私は何となく漫画を読んでいて、ただかっこよさそうだから無限という単語を使っているのかと思っていたが、本当はよく考えられていることを知り驚いた。(医)
物事を知っていると、漫画だって、楽しみに方に深みが増します。
1+1/2+1/4+1/8+…と無限に繰り返していくと最終的には2になるということだったが、個人的には,無限に続いても限りなく2に近い数字にはなるけれども、2になることはないのではないかと思った。(人文2ほか多数)
a = 1 + 1/2 + 1/4 +1/8 … とおくと、
2a = 2 + 1 + 1/2 + 1/4 … ですね(すべての項を2倍にする)。
ここで下の式から上の式を引くと、緑字の部分が同じなので、
a = 2
が導かれます。
無限に足すといっても、そうなると式はどれだけ長くなるのか不思議です。一番長い式はありますか(経)
「無限とは一番大きい数だ、という発想は愚考だ」という話が興味深かったです。(工)
「一番大きい数」や「一番長い式」は、存在しません。
証明には背理法を使います。
仮に一番大きい数や、一番長い式があったとして、それにもう一つだけ加えてやれば、そっちが一番大きくなってしまい、最初の仮定と矛盾するからです。
つまり、一番大きい数や一番長い式があるという仮定は立てられません。
私も、無限によって密になっていく瞬間が好きです。また極限の問題などで、分母が無限大に飛んでいく時はとても爽快です。(医)
先生が無限ファンとおっしゃっていてハッとしました。私も無限ファンです!(医)
無限の話が面白かった、ときめいた、分からなくなってきた、無限ファンの一歩を踏み出せた気がした、など。
二分法のパラドックス怖くないですか?説明はあっているはずなのに、実際にはそうならないことが起きている、なぜそんなことが起きるのか。考えれば考えるほど怖いです。(人文1)
私は無限が怖い。今回の講義を聞いているときにも無限の話を聞いているときは少し悪夢を見ているような感覚がした。(経1)
無限の話は、面白いと思ってツボる人とそうでない人に、わりとはっきり分かれます。
ツボった人は、この際、是非もっと深みにはまって、どツボってください。そんな人のために、講義の最後に面白いことを紹介しました。
自然数全体と偶数全体では、どちらの方がたくさんあるか?
きっと信じられないと思いますが、答えは「同じ」です。同様に、自然数と整数も同じです。このページの最後の動画に説明がありますよ。
ノイズ
滝や川の音がホワイトノイズに似ていると思ったのですが、それは水滴一粒一粒がぶつかった物や角度の違いによって、それぞれ違った周波数の音を出していて、無数に重なっているからそのように聞こえるという認識で良いのでしょうか。(人文)
ホワイトノイズを聞いたとき、雨のような音だなというふうに思った。ということは雨が降って雨粒がいろんなものに当たることでいろんな周波数の音がまじりあいホワイトノイズのようになっているのかなと思った。(工2)
素晴らしい。その通りですね。
少し補足すると、こうした自然界の音の場合、ホワイトノイズではなく、いわゆる1/fノイズと言われるタイプのノイズになるでしょう。1/fノイズとは、周波数が高くなるにつれて(周波数に反比例して)音の強さが弱まるスペクトルのノイズのことです。
光は赤、青、緑の三原色の組み合わせですべての色の光を作り出すことができると記憶していますが、音の場合も同様なものがあるのでしょうか?(経)
素晴らしい発想の質問ですが、そういうものはありません。どちらも物理学的には波動という点で共通ですが、光を感じる脳の仕組みと、音を感じる脳の仕組みは、ずいぶん違うので、何もかも同じということにはなりません。
全ての音を同じ時間に出すと全て打ち消されて無音になるのではないかと思った。(理)
同じ周波数どうしで、±を打ち消すようにすれば可能です。しかし、異なる周波数どうしの音は、絶対に、打ち消し合いません。時間とともに、ずれてくるからです
ピアノで例えば全鍵盤をを弾いてもホワイトノイズにはならないと思います。これは周波数が足りないからですか。(教)
そうです。半音より細い刻みで、全ての周波数を出さないといけません。
その他
ここ最近の講義を聞いてて思うのは、一つの分野を深く研究するには、多くの分野の知識が必要になるのだなということです。(理2)
皆さんは、音について勉強するだけで、すでに随分と物知りになりましたよね。
深く知るには、広く知る必要もある、ということです。
高校物理で周波数の異なる波は干渉してうなりが生じることを習ったが、今回矩形波や三角波を聞いた時うなりは感じなかった。(工)
うなりが生じるには、2つの周波数が互いに近い、という条件があります。例えば、400Hz と 405 Hzのように。
授業で示した倍音は周波数が近くないので、うなりは生じません。
楽器ごとに音色が変わることには納得できたのですが、同じ楽器でも演奏者によって音色が変わるのはなぜなのか分かりませんでした。(工)
錦織圭のラケットを使っているのにどうして強くなれないのか、みたいな質問ですね。
トライアングルひとつでさえ、プロと素人では違う音がします。どのように楽器を持ち、どの場所を、どのような強さで、どのような角度で叩き、そのあと、どのように響きを空間に伝えるか、といったこと全てが、音色に影響します。
ただ、質問者さんのような誤解が生まれる理由も理解できます。義務教育で使われるリコーダーや鍵盤ハーモニカなどの楽器は、誰もが簡単に、同じような音が出せるようにしてデザインしてあり、その結果、奏者による差が出にくくなっているからです。
漫画にも無限の概念が出てきてその教養を知らないと浅い楽しみ方しかできないというのには感考えさせられた。教養は勉強や社会生活などだけでなく娯楽にも関わってくることは今まで考えたことがなかったのでなるほどなと思った。(工)
教養とは、ものの見方そのものです。
新しいメガネをかけるようなもので、あらゆる面で、世界の見え方が変わってきます。
以前は分からないことをひたすら考えることが嫌いだったのですが、最近考えることが増えたからか今日の授業で無限について聞いたり考えたりするほど益々分からなくなっているにもかかわらず、それはそれで面白いと初めて思えました。(農)
皆様のおかげで、質問意識が強くなっていると感じた。(国セ1)
嬉しいコメントです。みなさん確実に成長していますね!
円周率は円周÷半径で定義したほうが数学的に美しいという話をご存知でしょうか。電流の定義といい、こうした科学の不都合は一周回って発展したからこそ起こりえたのだと感慨深く感ぜられます。
無限についての以前見た動画があったので共有しておきます。(工2)
https://www.youtube.com/watch?v=7C5-koMd-_A
どちらも素晴らしい動画資料ですね。数学好きには、たまらないでしょう。


